전문 전자기술자료 제공(고주파회로 기초강좌)

지금, 우리 주변에는 이동통신기기를 비롯하여 고주파 회로를 이용한 장치가 무수히 넘치고 있다. 아날로그 회로 뿐만 아니라, 디지털 회로에도 고주파 회로 기술이 더욱 요구되는 시대가 되었다. 여기서는 이러한 시대의 요구에 대응하여 실제 고주파 회로를 설계하고 , 제작, 조정이라고 하는 실무적인 시점에서 초보자를 대상으로 해설한다.

우선 먼저, 여기서는 UHF대 이상을 고주파라 부르기로 한다(주파수로는 300MHz 이상, 자유공간의 파장에서는 약 1m 이하).
고주파라고 하면 무엇인가 특별한 영역이라고 생각하는 사람도 있을 지도 모르지만, 사실 일반적으로 취급하는 경우가 많은 저주파 교류회로가 오히려 특수한 것이다.
무엇 때문일까? 교류신호는 주파수의 역수에 비례하는 파장을 가지고 있다. 저주파의 경우, 예를 들면 1MHz 신호의 자유공간에 있어서의 파장는 약 300m이다. FR-4 기판상에서도 그 파장는 약 137m나 된다. 아무리 기판이 크다고 해도 수십 cm 정도이므로, 1MHz의 신호를 취급하는 회로를 설계하는 경우에, 그 파장을 전혀 의식하는 일없이, 무시하고 설계하고 있는 것이다. 즉 근사를 하고 있는 것이다.

그러면 취급하는 신호의 주파수가 1GHz로 되면 어떻게 될까?. 자유공간에서의 파장은 1MHz의 1/1000인 30cm로, FR-4 기판상에서는 겨우 13.7cm로 되고 만다. 취급하는 신호의 파장에 대하여 기판상의 패턴 길이를 무시할 수 없게 된다. 단순한 라인에서도 라인상의 위치가 수 cm 차이가 있을 뿐이며, 신호의 위상과 진폭이 전혀 다르다.

고주파의 경우, 저주파와 같이 오실로스코프를 이용하여 간단히 전압 파형을 관찰할 수 없다. 따라서 전류, 전압으로 고주파 회로 특성을 측정하는 것은 거의 불가능하기 때문에, 전류와 전압의 곱인 전력으로 회로특성을 측정한다. 사용하는 단위는 W가 아니라, dBm(0dBm=1mW)을 주로 사용한다.

고주파 회로에서는 전력을 어떻게 효율적으로 전달할 것인가 하는 점이 중요하다. 전력을 효율적으로 전달하기 위해서는 임피던스를 정합시킬 필요가 있다. 고주파 회로에서 임피던스라고 하면 특성 임피던스를 가리킨다.(임피던스 정합, 특성 임피던스에 대해서는 전기회로의 문헌을 참조하기 바란다)

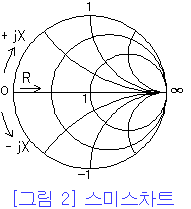
2. 스미스차트(Smith chart)

서론이 상당히 길어졌는데, 그러면 스미스차트(Smith chart)에 대한 이야기를 시작하기로 한다. 전기 관련의 문헌이나 서적에서 스미스차트를 조사하면 "Z평면에서 R≥0 범위의 R=일정, X=일정한 직선군을 Γ 평면에 사상(寫像)한 도표,……"라는 식으로 설명이 쓰여져 있을 것으로 생각한다.
직교 좌표계를 둥근 변형된 도표에 사상한 것 뿐이라고 생각할 지도 모르지만, 이것이 임피던스 변환에 매우 유용한 것이다. 스미스차트를 이용하면 번거로운 계산을 하지 않아도 임피던스 변환을 기하학적으로 구할 수 있다.
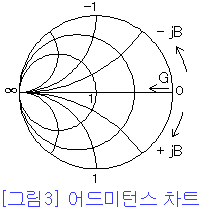
Smith chart는 임피던스와 반사계수와의 관계를 도표화한 것으로, 직렬회로(소자)의 취급에 적합하다. 병렬회로(소자)를 취급하는 경우에는 어드미턴스(admittance)로 생각하는 편이 간단하다.
어드미턴스와 반사계수와의 관계를 도표화한 것을 어드미턴스 차트(admittance chart)라 부른다. 더구나, 스미스차트와 어드미턴스 차트를 서로 겹쳐 작성한 것은 이미턴스 차트(immitance chart)라 부른다.
차트상에서는 임피던스(또는 어드미턴스)를 기준이 되는 특성 임피던스로 정규화하여 표시한다. 여기서 취급하는 주파수대에서는 대부분의 경우 특성 임피던스 50Ω을 기준으로 하고 있다.
(예 :25+j10Ω → 0.5+j0.2)

Z평면으로부터의 사상 등, 스미스차트에 대한 상세한 설명은 다른 서적이나 문헌을 읽기 바라며, 여기서는 스미스차트상에서 임피던스 궤적의 움직임을 살펴 보기로 한다.